BWM算法浅析-FM(二)
注意:由于用语言不好描述,故使用图表结合的方法进行解释,点击图可直接查看原图,点开后右上角有关闭按钮!
一、FM-index 简介
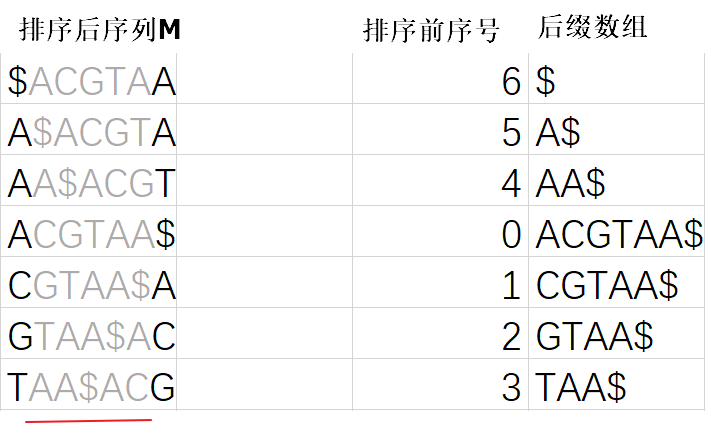
fm-index是一种结合到BWT和小的辅助数据结构中的索引,它的核心就是BWM中的F与L(不了解的可查看我的上一篇文章)。虽然BWM与后缀数组有关,但是不能使用与后缀数组相同的查询方法,因为字符串的中间部分我们并没有进行保存。这里我们使用上一篇文章所用的字符串S(ACGTAA)作为示范。见下图所示,其中红线部分未保存。
二、FM Index 查询
当我们需要查询子字符串P在字典序排序矩阵M中行的范围时,我们可以以P的最短后缀开始查找,直到P扩展完成或者行的范围为空为止。例如:
第一次查找
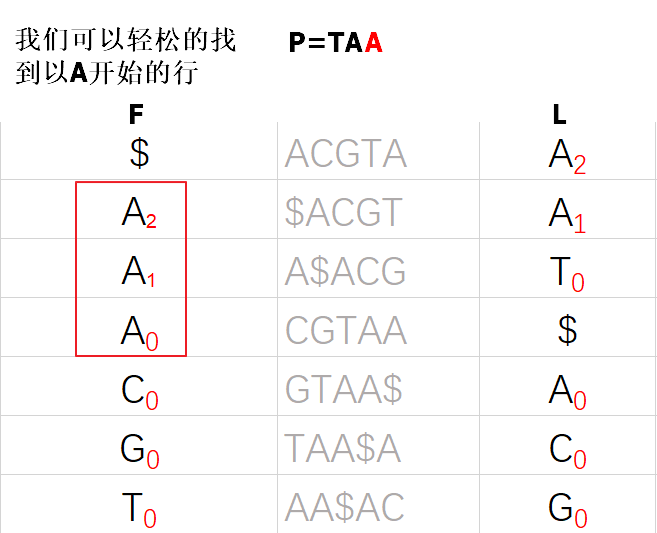
第二次查找
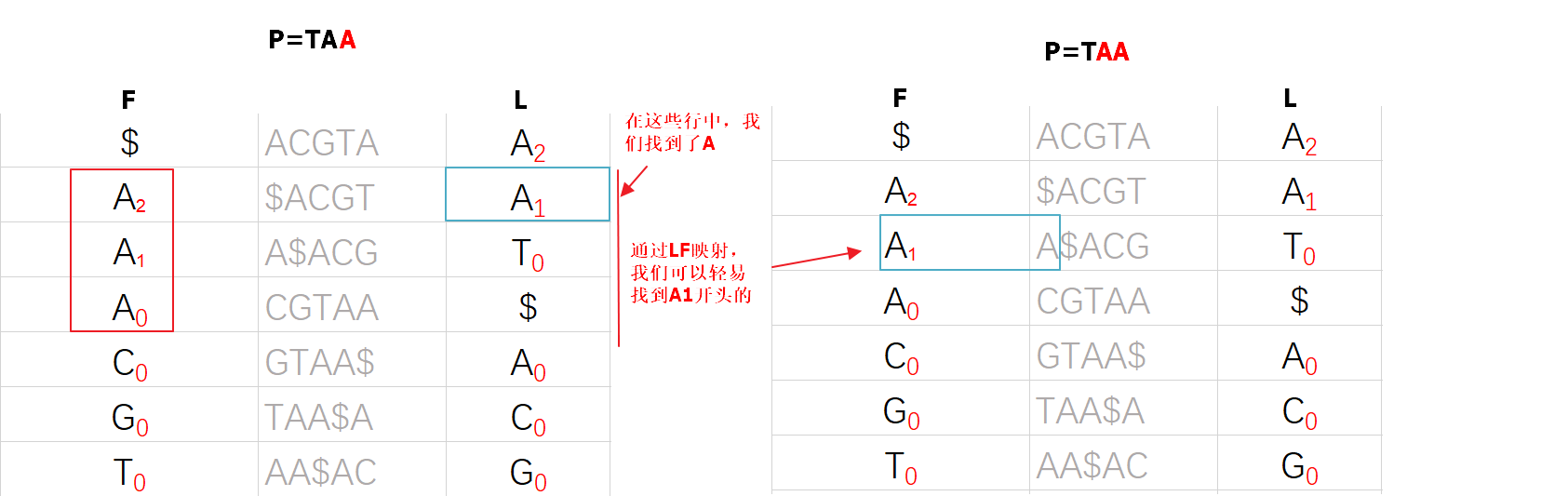
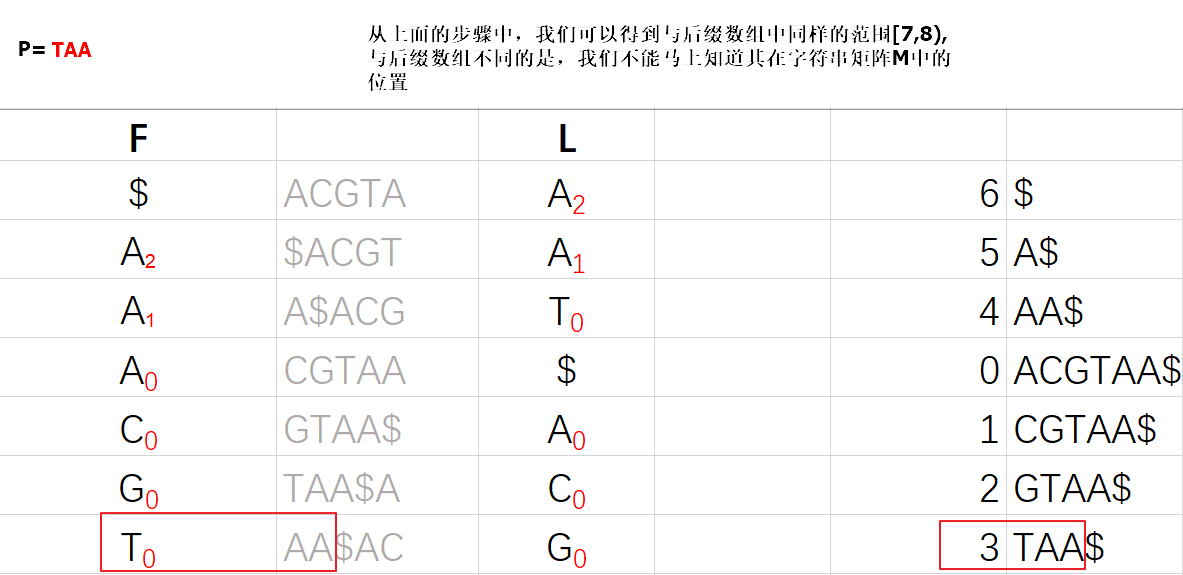
现在我们找到了AA后缀的行,接下来,我们开始查找TAA后缀的行

当子字符串P不在S中时,我们在L列中是找不到下一个字符的,例如:
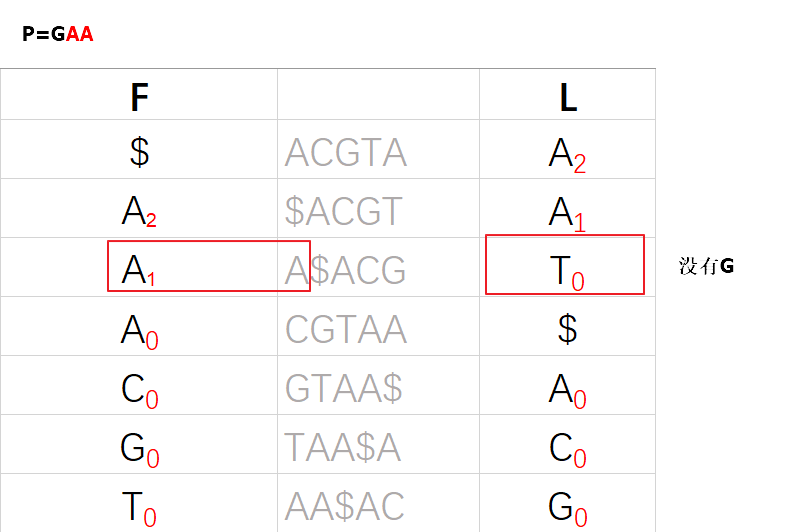
三、FM-index 存在的问题及解决方法
在上面介绍的方法中,还存在这几个问题:
- 扫描字符速度较慢,算法时间O(m);
- 存储字符的出现次数需要大量的内存空间;
- 需要确定字符串P在S中的具体位置
是否有算法时间O(1)的方法进行排名的计算呢?
快速计算排名
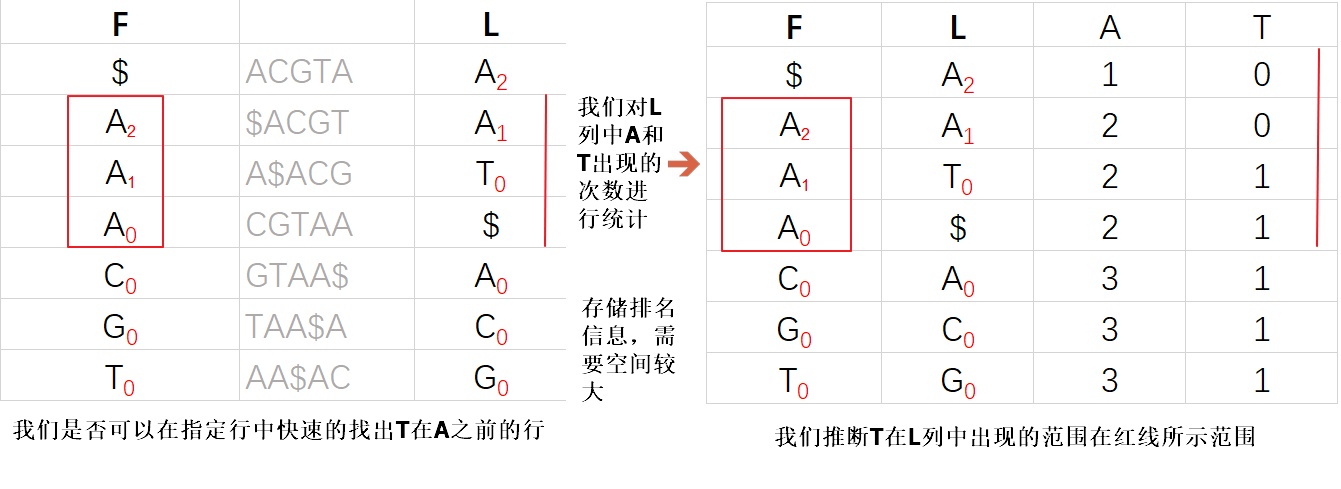
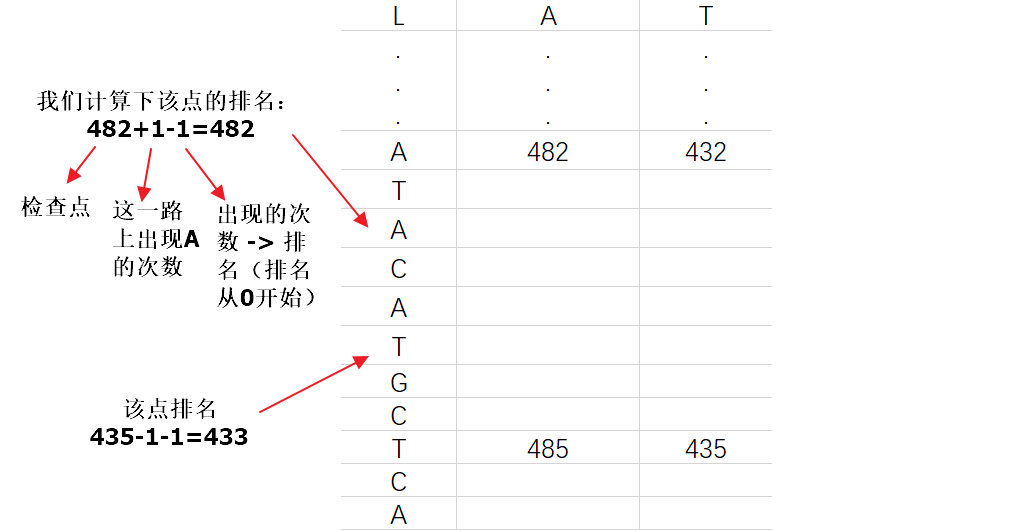
上诉方法虽然时间复杂度是O(1),但是需要额外的空间来存储排名信息,下面我们考虑在存储排名信息时,仅存储部分信息,以减少空间消耗,为了追踪到所有排名信息,每个一段距离设置一个检查点(checkpoints)

如何计算排名呢?
当前已经解决的问题有:
通过存储字符出现的次数和设置检查点,我们解决了扫描字符速度过慢,存储需要消耗过大的存储的问题
目前还需要确定字符串P在S中的具体位置
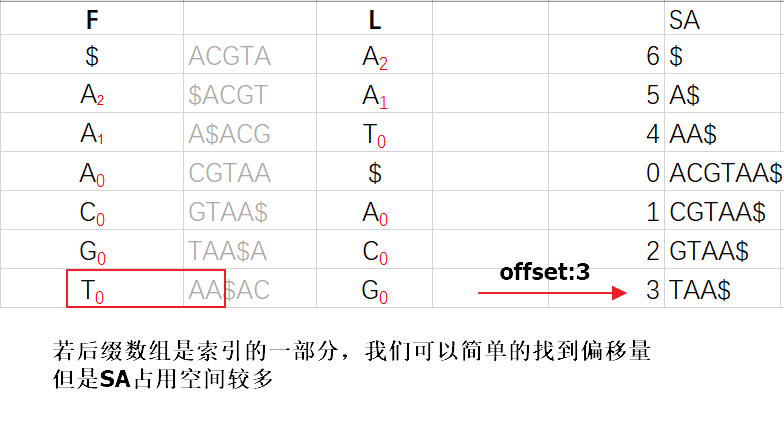
由于SA也需要大量空间来进行存储,这里我们仍然使用存储部分数据的方法来减少所需存储。
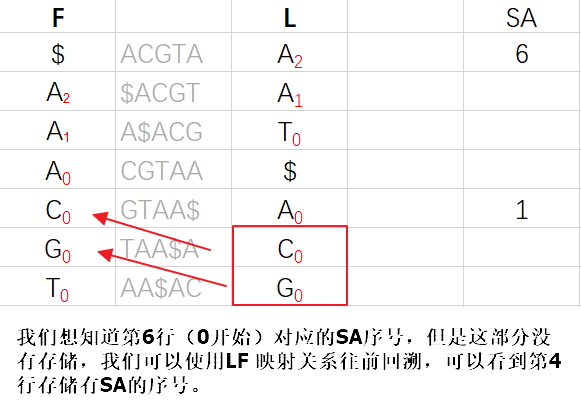
所以第6行所对应的SA序号值x = 1(第四行SA的序号值)+2(回溯步数) = 3
至此,所有问题均解决了!
参考
版权声明:本文转载请注明出处!



最新评论:
发表评论
电子邮件地址不会被公开。 必填项已用*标注