BWT算法浅析-(一)
一、前言
BWT算法对数据量大的数据来说,压缩比较有效,目前已经广泛用于生物学数据的存储中,例如bowtie就使用到了这一策略。虽然之前在大学期间学过该算法,但是有点遗忘了,故重新复习一番。
二、什么是BWT?
严格来说,BWT并不是压缩算法,它仅是把需要压缩的字符重新排列,将相同的字符排在一起或者相邻位置,使其更易被压缩。
三、BWT原理
BWT算法主要分为两个部分,编码以及解码。
3.1、编码
编码过程主要分为3个步骤:
1. 循环待压缩字符,构建字符矩阵M; 2. 按照字典序重排矩阵M; 3. 提取重排后的矩阵M的最后一列L;
下面我们举个例子来说明,假如我们需要压缩字符串S是ACGTAA。
首先,我们在该字符后添加一个字符$(该字符不存在于字符串S中,且其ASCII码小于字符串S中的任意一个字符,思考一下为什么呢?),然后将当前字符串的第一个字符移到最后一位,形成一个新的字符串,再将新的字符串的第一位移到最后一位形成另一个新的字符串,就这样不断循环这个过程,直到字符串循环完毕(即$处于第一位),这样就形成了一个基于原字符串的字符矩阵。这里我们使用python代码来进行实现:
def rotations(s):
s_mat = []
for i in range(0, len(s)):
tmp = s[i:]+s[:i]
s_mat.append(tmp)
return s_mat
接下来就是按照字典序排序矩阵M,这个比较简单,就不多说了,在python中直接sort即可。矩阵如下,其中F列为矩阵第一列,L列为矩阵最后一列
| ID | rotations | sort | F | L |
|---|---|---|---|---|
| 1 | ACGTAA$ | $ACGTAA | $ | A |
| 2 | CGTAA$A | A$ACGTA | A | A |
| 3 | GTAA$AC | AA$ACGT | A | T |
| 4 | TAA$ACG | ACGTAA$ | A | $ |
| 5 | AA$ACGT | CGTAA$A | C | A |
| 6 | A$ACGTA | GTAA$AC | G | C |
| 7 | $ACGTAA | TAA$ACG | T | G |
3.2、解码
解码主要是通过L列还原到原来字符串,其主要原理是通过LF列对应关系进行还原。为了方便说明,我们给每个出现的字符一个编号,表示当前字符出现了几次,原字符串为A0C0G0T0A1A2。
| Sort | F | L |
|---|---|---|
| $0A0C0G0T0A1A2 | $0 | A2 |
| A2$0A0C0G0T0A1 | A2 | A1 |
| A1A2$0A0C0G0T0 | A1 | T0 |
| A0C0G0T0A1A2$0 | A0 | $0 |
| C0G0T0A1A2$0A0 | C0 | A0 |
| G0T0A1A2$0A0C0 | G0 | C0 |
| T0A1A2$0A0C0G0 | T0 | G0 |
从上表中可以看出,F列中对应字符出现的顺序与L列中一致,例如:F列中A2A1A0与L列中A的出现顺序一致。并且在原字符串S中,L列是F列的前一个字符。我们根据该规则即可向前回溯得到原字符。回溯过程如下图所示:
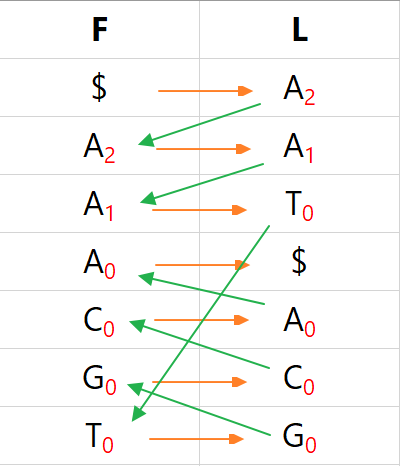
最终我们可以得到字符串A2A1T0G0C0A0$,将该字符串反转就是我们的原字符S了。Python代码实现如下:
#!/usr/bin/env python3
# encoding: utf-8
"""
@author: burning
@software: pycharm
@file: decode_bwm.py
@time: 2020/5/25 20:54
@desc:
"""
def L_rank(rev_str):
total_num = {} # 字符出现的总次数,1开始
ranks = [] # 每个字符第几次出现,0开始
for i in rev_str: # 循环每个字符
if i not in total_num: # 当前字符未出现过
total_num[i] = 0
ranks.append(total_num[i]) # 添加当前字符第几次出现
total_num[i] += 1 # 当前字符出现次数加1
return total_num, ranks
def firstCol(total_num): # 获取F列
first = {}
total_c = 0
for c, count in sorted(total_num.items()): # 遍历排序后的L列
first[c] = (total_c, total_c+count) # 保存当前字符在F列中出现的位置范围
total_c += count # 下一个字符起始位置
return first
def reverse(str_L):
total_num, ranks = L_rank(str_L)
str_F = firstCol(total_num)
result="$" # 最终结果
start_row = 0 # 起始行
while str_L[start_row] != "$": # 非结束
c = str_L[start_row] # 当前字符
result = c + result # 回溯所得结果
start_row = str_F[c][0] + ranks[start_row]
return result
问答:
1、为什么通过转换后可以提高压缩水平?
答:因为转换后,大量相同字符将靠近,压缩时将会减少大量空间,例如:假设ATGC 在待压缩字符中大量存在,则通过该算法转换后,以TGC开头的字符串在排序后将会靠在一起,其最后的一个字符是A也会靠近在一起。
PS:还有部分是FM-index的原理,下次有机会再写了!



最新评论:
发表评论
电子邮件地址不会被公开。 必填项已用*标注