在机器学习中，我们常用到特征选择算法，好的特征对于模型来说，能得到更好的结果。特征选择的好处包括但不限于：

1. 降低数据的维度以降低计算复杂度；
2. 降低噪声以提高分类准确性；

特征选择方法主要有3个类别：

1. 过滤法（filters）：过滤法本质上是数据预处理和数据过滤方法，特征的选择主要是基于内在特征进行挑选的，例如相关性、判别目标类别的能力、互信息等。其比较容易计算也比较有效，有比较好的泛化能力；
2. 包装法（wrappers）：包装法是基于学习方法的包装，可选择出对学习方法较好的一组特征。通常需要大量的计算选择最好的特征；
3. 嵌入法（embedded）：嵌入法将特征选择的机器学习模型的训练过程相结合，基于特征权重值来挑选最优子集；

下面我们将简单介绍下最小冗余最大相关算法（mRMR）

mRMR

mRMR算法也是过滤法的一种，其希望得到这样的一个特征子集：

• 1）对于相同大小的特征子集来说，mRMR方法挑选出的子集对于目标性状来说更有代表性；
• 2）mRMR方法挑选的子集与原先的大数据集在性能上相差不大；

mRMR使用互信息作为两个基因（特征）间相关性的度量，其中用I表示互信息。互信息是信息论中的一个概念，其量化了两个变量间的相互依赖程度。

离散变量

对于离散/分类变量来说，

等式一

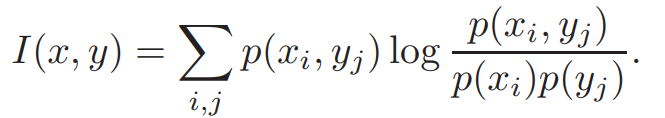
其中x与y分别表示两个不同的特征，p(x,y)为x,y的联合概率分布，p(x)和p(y)分别为对应的边际概率。

使用互信息来衡量特征间的相似性，最小冗余的特征集是选择其互信息最大的特征组成的，用S表示我们寻找的最小冗余的特征子集，则

等式二

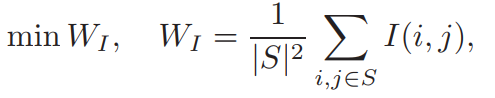
其中，为了符号简洁，我们使用I(i,j)表示I(g_i,g_j),|S|(=m)表示特征S的数量。

为了衡量特征对目标类别的判别能力，我们再一次的使用互信息来衡量，则最大的相关条件可以表示如下：

等式三

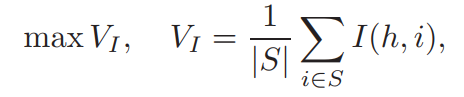
其中h表示目标类别，I(h,g_i)量化了的g_i对分类任务的相关性，为简洁表示，这里用I(h,i)表示。

特征子集可以通过min W_I 和max V_I同时获得，为了优化这两个条件，将两者视为同等重要，考虑两种最简单的组合：

等式四

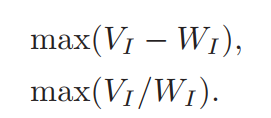
此算法的时间复杂度为O(N^|S|),其中N是整个特征集Ω的特征数量。为了优化时间复杂度，作者采用了启发式算法：

• 1） 采用等式三选择第一个特征，该特征有最高的I(h,i)；
• 2） 剩余的特征采用增量方式进行获取：

早期选择的特征，留在特征集中，假设m个特征已经选择到特征集S中，则余下的特征将从Ω_S = Ω - S（等同于除去已选特征外的所有特征）中获取。优化后的两个公式如下：

等式五

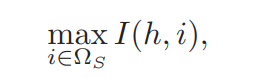
等式六

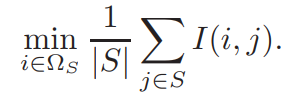
等式五相当于是等式三（最大相关性条件），等式六相等于等式二，是最小冗余的一个近似解。这两个等式可以近似等于等式五，故此，得到了一个新的选择标准：

1. MID: 互信息差 
2. MIQ: 互信息商

优化后的公式计算复杂度为：O(|S|*N)

连续变量

对于连续的数据变量或属性，我们可以使用使用特征与目标分类的F统计量作为最大相关性衡量标准

等式七

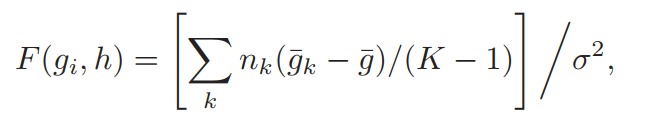
其中，g_i​为特征，h为目标类别，K表示类别数，g^¯表示所有样本的特征g_i​的均值，g_​k​^—是第k类目标的g_i​的均值，σ²是方差，可用下述式子表示

等式八

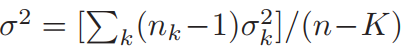
其中n_k​和​ σ_k分别是第k类的大小和方差。由于F=t², 对于二分类，可将F检验转为T检验。对于特征子集S，最大相关性公式如下：

等式九

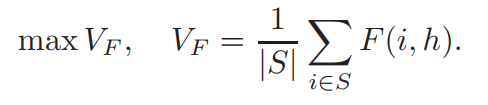
对于最小冗余条件，我们使用皮尔逊相关系数 c(g_i,g_j)=c(i,j)，则对应的最小冗余公式为：

等式十

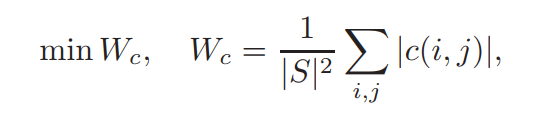
这里取绝对值是因为相关性不管正负高度相关时，均认为是冗余。也可以使用欧氏距离来替代相关性，不过作者的实验证明相关性效果更好。最终得到优化后的标准如下：

1. FCD：使用差结合F检验和相关性结果
2. FCQ：使用商结合F检验和相关性结果

综上所述，最终的算法可如下表所示：

参考：

1. [1]孙广路等. "基于最大信息系数和近似马尔科夫毯的特征选择方法." 自动化学报 43.5(2017):11.
2. Ding, Chris, and Hanchuan Peng. “Minimum redundancy feature selection from microarray gene expression data.” Journal of bioinformatics and computational biology vol. 3,2 (2005): 185-205. doi:10.1142/s0219720005001004